Normalverteilung
Für wachsenden Stichprobenumfang nähert sich jede Verteilung beliebig der Normalverteilung an. Die Parameter der mit dem griechischen Buchstaben φ (phi) bezeichneten Dichtefunktion sind der Erwartungs- bzw. Mittelwert μ (my) und die Standardabweichung σ (sigma). Man bezeichnet eine Normalverteilung häufig auch mit N(μ,σ). Der Spezialfall N(0,1) ist die Standardnormalverteilung. Da es keine geschlossene Formel für die Verteilungsfunktion Φ (Phi) gibt, schreibt man direkt das Integral über die Dichtefunktion explizit hin. Die deswegen nicht so einfach berechenbaren Funktionswerte bietet man häufig, etwa in Statistiklehrbüchern, in Tabellenform an.
Hier können Sie die Parameter und das Erscheinungsbild der Normalverteilung variieren und die Graphik bei Bedarf kopieren.
In der Mathematik bedeutet das Integral die Fläche unterhalb einer Kurve in den angegebenen Grenzen. Für einen kurzen und knappen Überblick klicken Sie bitte auf meine Folien zur Differenzial- und Integralrechnung. Diese können natürlich weder einen Unterricht noch ein Lehrbuch ersetzen.
| Normalverteilungsdichte | Normalverteilungsfunktion |
|---|---|
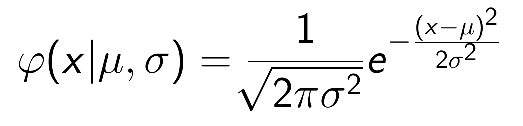 |
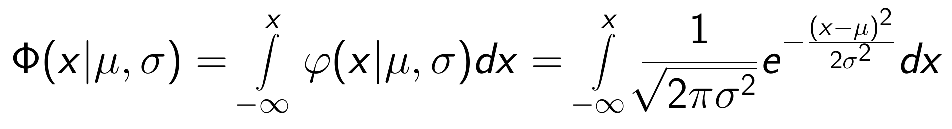 |