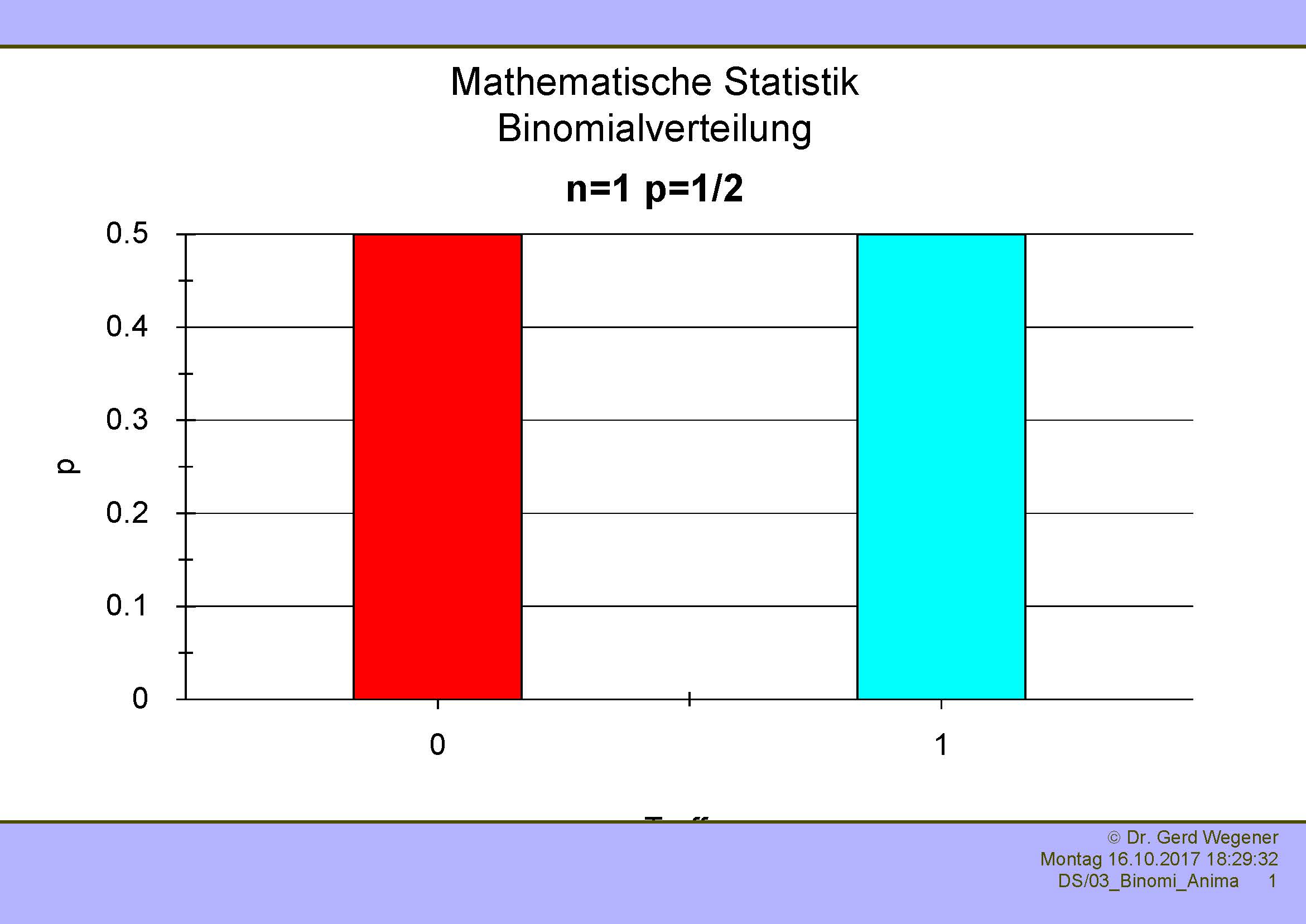
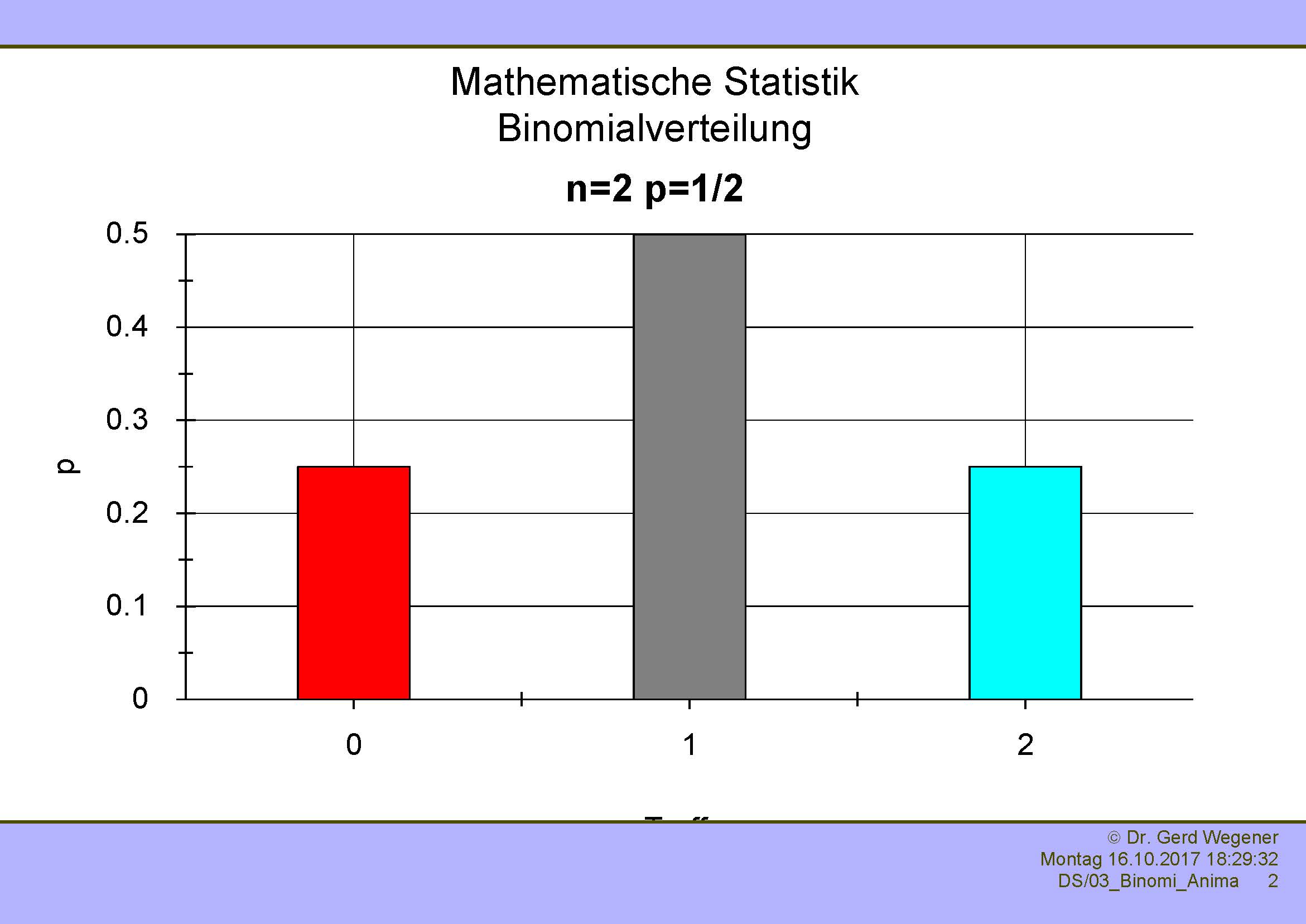
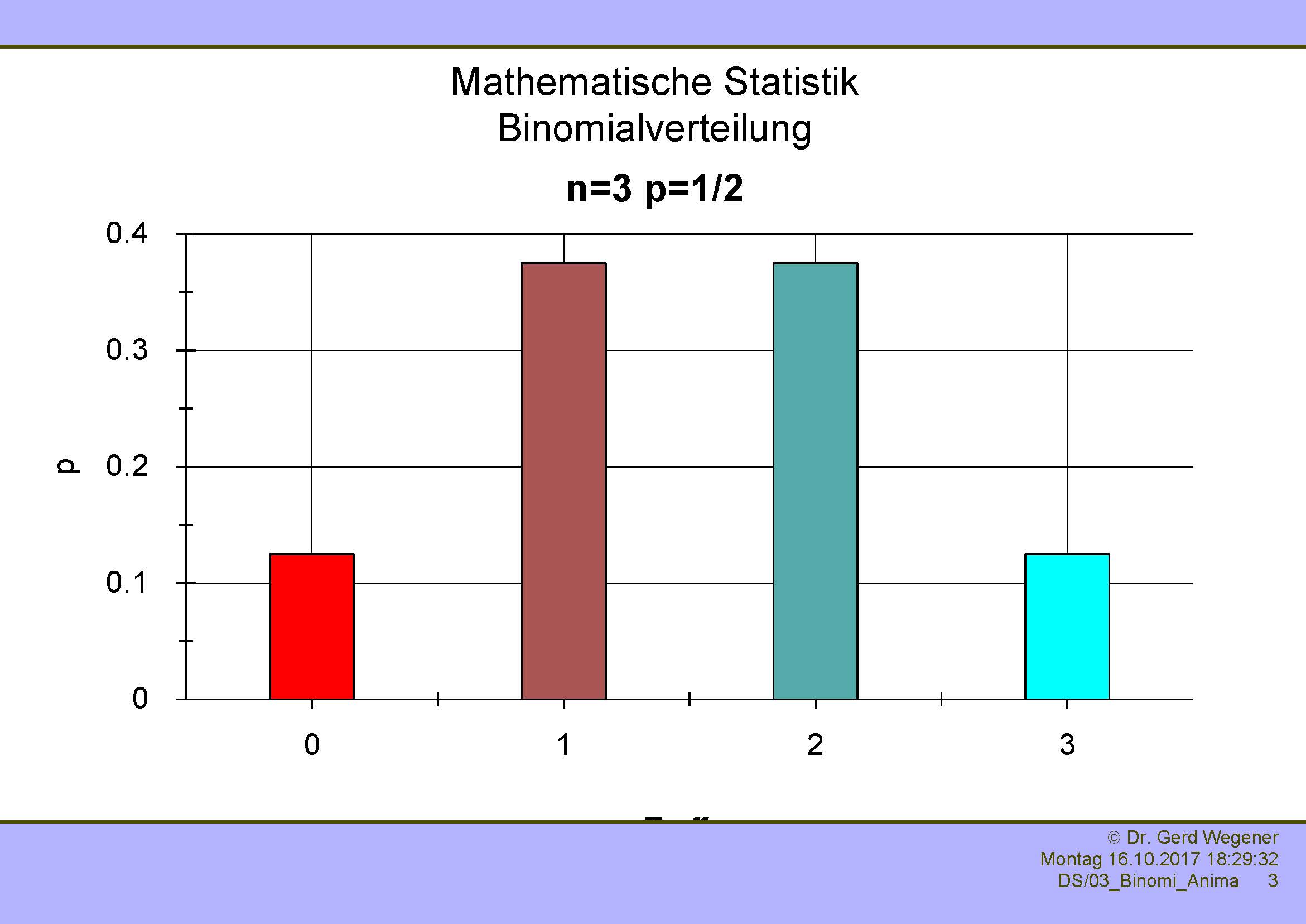
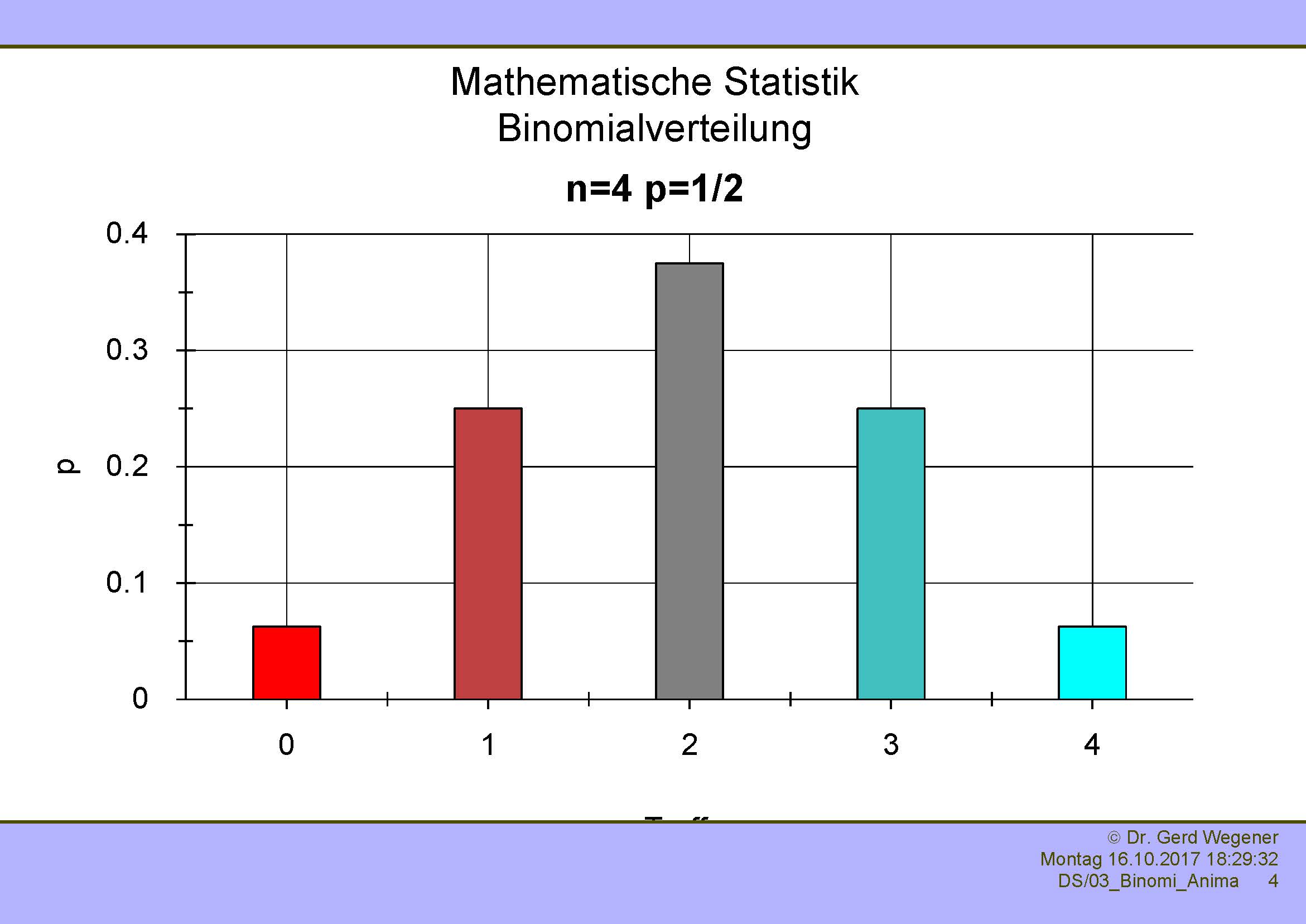
Immer wenn ein Experiment oder Versuch mit binärem Ausgang ("Treffer" oder "kein Treffer") unabhängig wiederholt wird, ergibt sich eine Binomialverteilung. Die Parameter einer solchen Verteilung sind die Wahrscheinlichkeit p und die Anzahl der Versuche n.
Die folgenden Abbildungen zeigen die Binomialverteilung mit Wahrscheinlichkeit p=1/2 und verschiedenen n von 1 bis 4. Der erste Balken zeigt die Wahrscheinlichkeit, bei n Versuchen kein einziges Mal einen Treffer zu haben. Der zweite Balken zeigt die Wahrscheinlichkeit, genau einen Treffer zu haben, der dritte genau zwei, der vierte genau drei, etc.
 |
 |
 |
 |
Hier wird eine Binomialverteilung mit p=1/2 und n von 1 bis 100 laufend gezeigt. Ihr Browser muss dazu aktive Elemente zulassen. Tut er das nicht, können Sie sich hier das zugehörige pdf ansehen.
Etwas anders sieht es aus, wenn die Wahrscheinlichkeit p=1/6 beträgt. Nachfolgend sehen Sie diese Binomialverteilung für n=1, 2, 5 und 10.
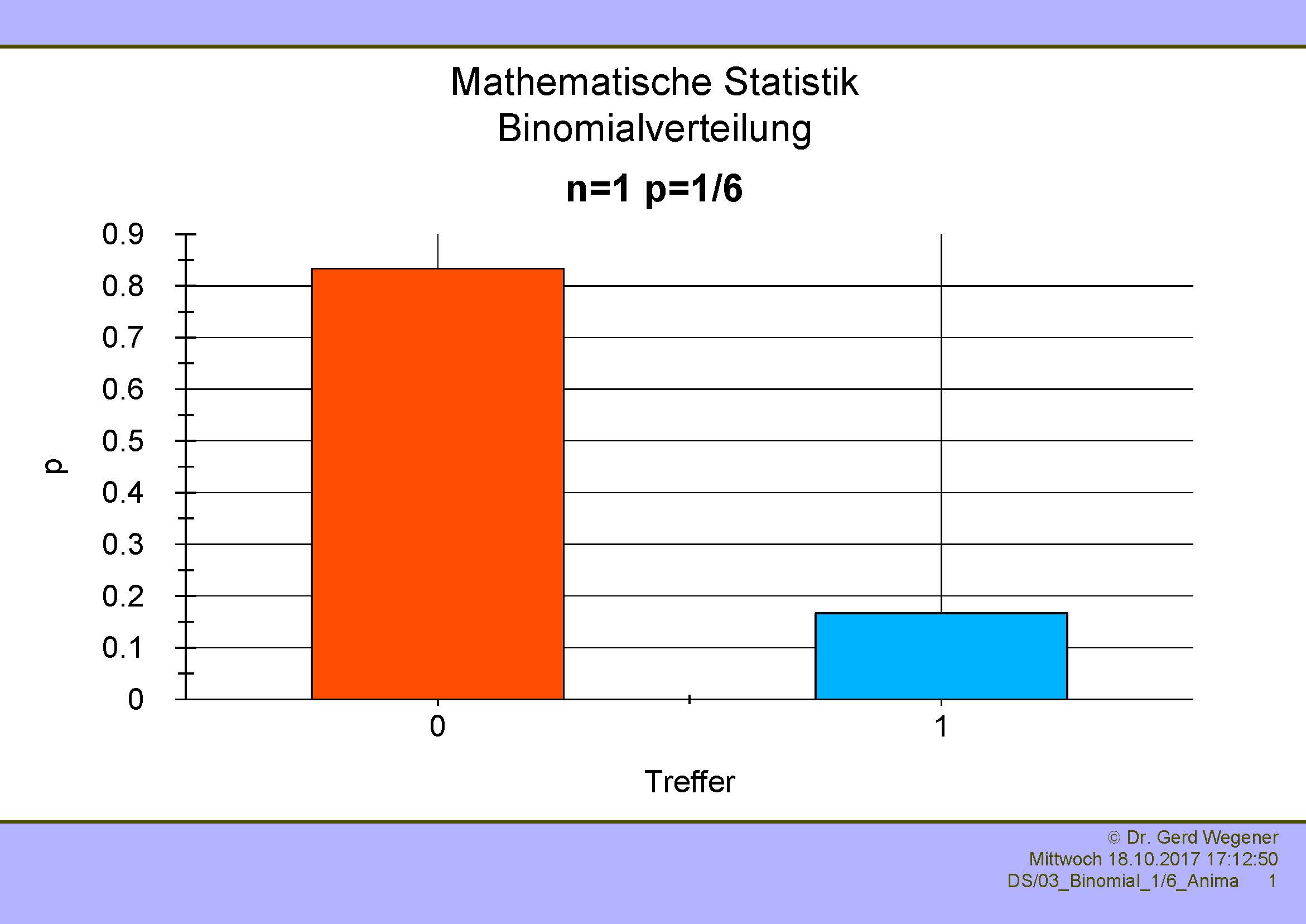 |
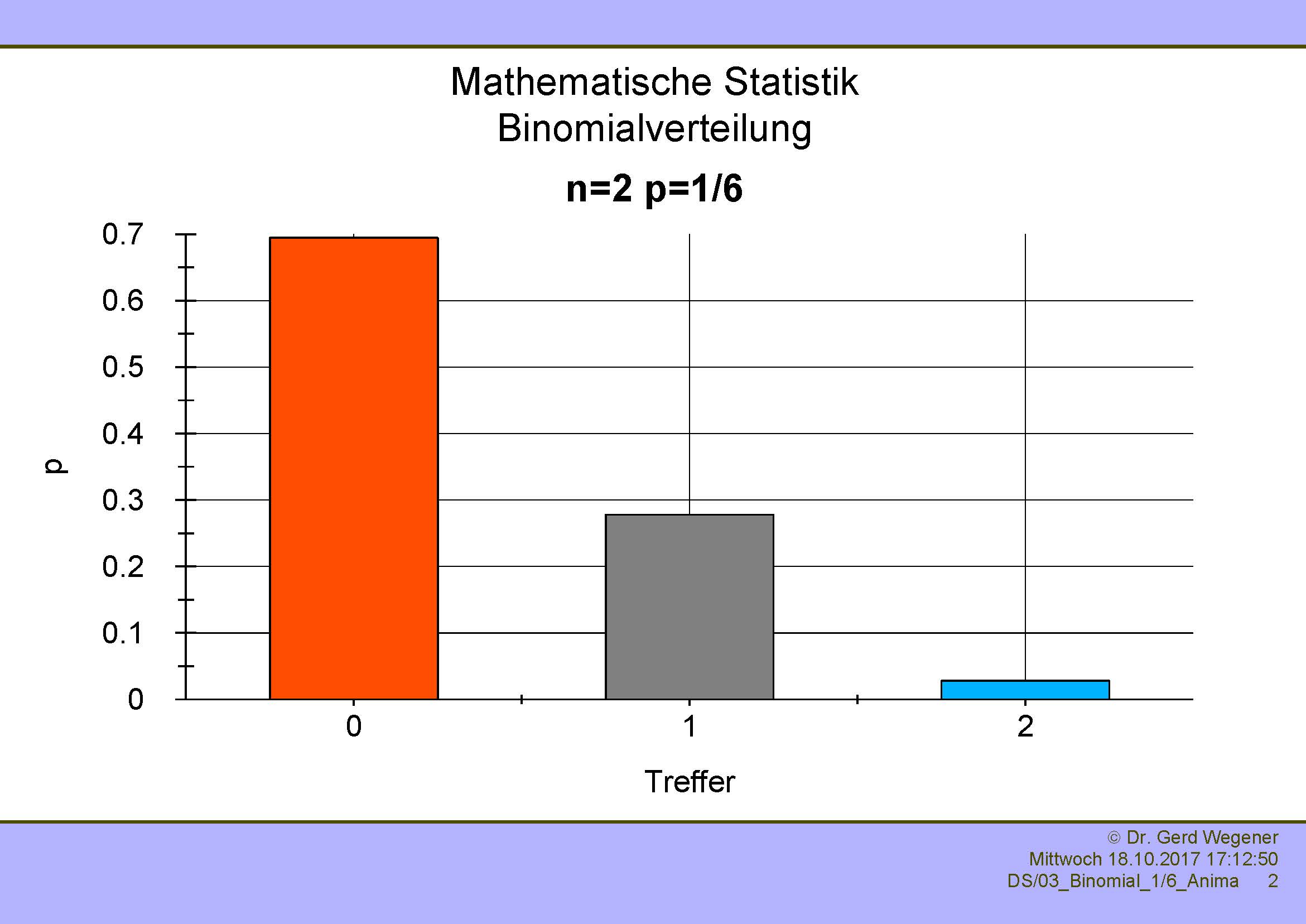 |
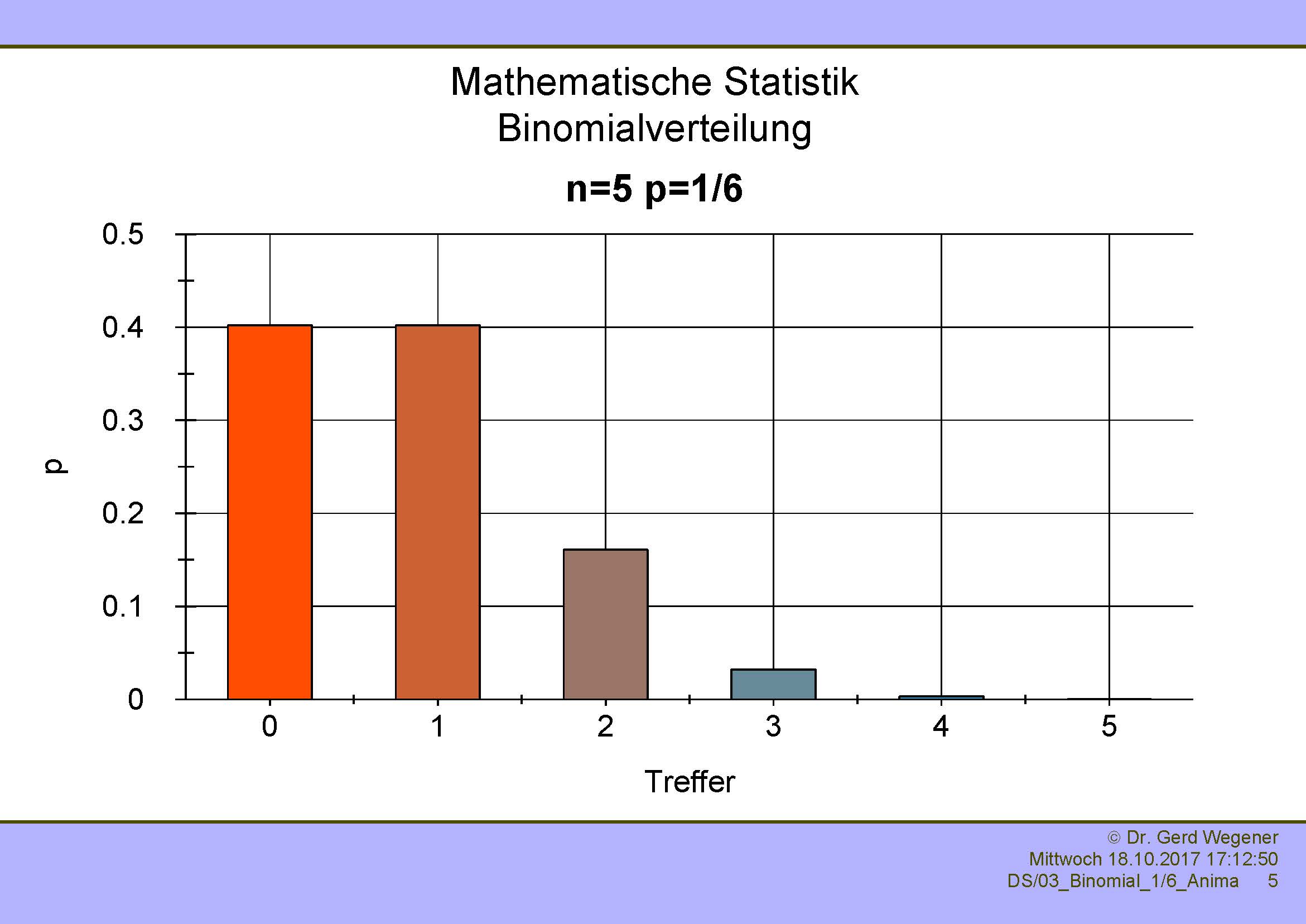 |
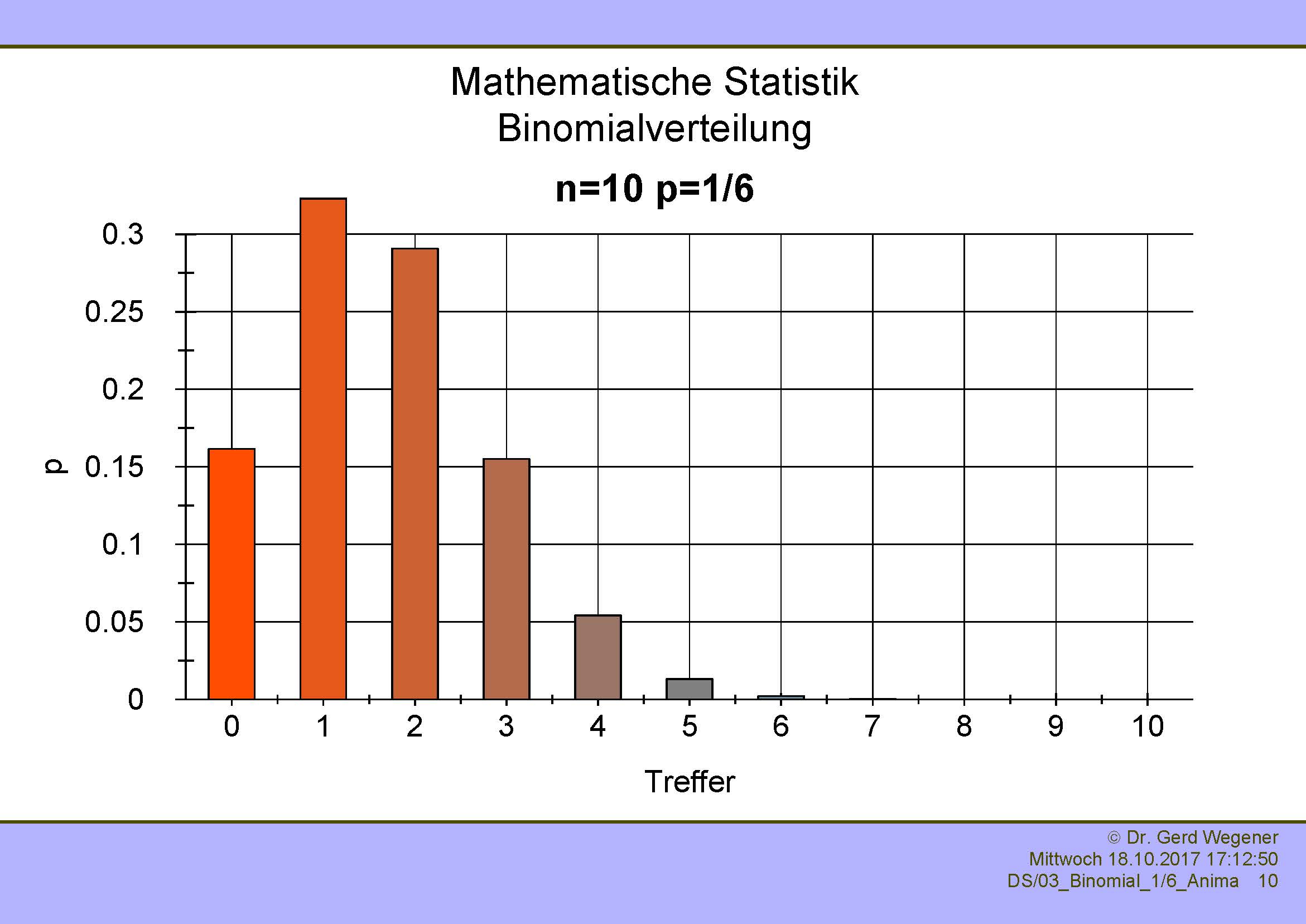 |
Nach dem zentralen Grenzwertsatz nähert sich jede Verteilung mit wachsendem Stichprobenumfang beliebig der Normalverteilung an. Dieses verdeutlichen drei Binomialverteilungen mit p=1/2, p=1/6 und p=3/4. Die zugehörige Normalverteilung ist in grün eingezeichnet. Alternativ das Ganze als pdf hier für p=1/2, p=1/6 und p=3/4.
Die Annäherung an die Normalverteilung lässt sich auch gut ablesen, wenn man statt n das p variiert. Hier einmal für n=20 und einmal für n=50. Alternativ als pdf für n=20 und einmal für n=50.
©Dr. Gerd Wegener, Hannover 2020.